Mengenal Analisis Korelasi
Bagi kamu yang pernah belajar ilmu statistika, pasti tidak asing dengan materi analisis korelasi. Korelasi merupakan salah satu cara dalam ilmu statistik yang banyak dipakai untuk mengukur hubungan antara dua variabel yang bersifat kuantitatif.
Analisis Korelasi merupakan studi yang membahas tentang derajat hubungan atau kekuatan asosiasi linier antara dua variabel, misalnya variabel x dan variabel y. Korelasi tidak menunjukkan hubungan fungsional, atau dengan kata lain, ia tidak membedakan antara variabel dependen dan variabel independen.
Hubungan antarvariabel yang saling berkorelasi tidak secara otomatis menunjukkan adanya hubungan sebab akibat atau timbal balik. Misalnya saja penggunaan analisis korelasi linier sederhana untuk mengetahui kekuatan hubungan antara besarnya pendapatan dan kekayaan, atau mengetahui kekuatan hubungan antara motivasi kerja dengan produktivitas kerja.
Dalam suatu penelitian, seorang peneliti senantiasa berusaha mengungkapkan hubungan/korelasi antara beberapa fenomena alami (variabel). Variabel yang dimaksud dapat berupa variabel kualitatif maupun variabel kuantitatif. Variabel x dan variabel y dinyatakan mempunyai korelasi apabila x dan y mempunyai perubahan variasi yang satu sama lain berhubungan. Artinya, jika variabel x berubah, maka variabel y pun berubah.
Apabila variabel x merupakan sebuah variabel yang sifatnya menerangkan tingkah laku variabel y, maka variabel x disebut variabel bebas (independent variable). Apabila variabel y tingkah lakunya diterangkan oleh variabel x, maka variabel y disebut variabel tak bebas (dependent variable) atau penyebab.
Dalam tulisan ini akan dibahas korelasi antara dua variabel yang keduanya mempunyai dua pengukuran interval/rasio. Hubungan yang paling sederhana antara dua buah variabel x dan variabel y masing-masing mempunyai tingkat pengukuran sekurang-kurangnya jenis datanya interval. Data interval adalah tingkat pengukuran dengan jarak atau interval yang sama. Tingkat hubungan linier antara variabel x dan variabel y bisa digambarkan oleh sebuah bilangan yang disebut Koefisien Korelasi.
Metode Penghitungan Koefisien Korelasi
Sebenarnya, banyak metode yang bisa digunakan untuk menghitung koefisien korelasi, bergantung pada tingkat/skala pengukuran variabel x dan variabel y. Jenis-jenis korelasi tersebut antara lain:
-
Korelasi Pearson (Pearson Correlation)
Korelasi Pearson adalah jenis korelasi yang digunakan untuk mengukur hubungan di antara hasil-hasil suatu pengamatan dari populasi dengan 2 varian (bivariate), berdistribusi normal. Analisis ini sering digunakan untuk variabel berskala interval dan rasio.
Koefisien korelasi yang menyatakan hubungan linier antara dua buah variabel x dan variabel y masing-masing mempunyai data dengan tingkat pengukuran sekurang-kurangnya interval, didefinisikan sebagai berikut.
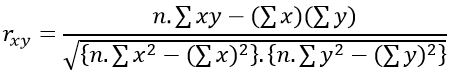
Keterangan:
rxy = koefisien korelasi variabel x dan y
n = banyak pasangan variabel x dan y
-
Korelasi Spearman (Spearman Correlation)
Korelasi Spearman yaitu korelasi yang dipakai untuk mengukur keeratan hubungan antara hasil pengamatan dari populasi yang memiliki 2 varian yang berdistribusi tidak normal. Biasanya jenis korelasi ini digunakan untuk data berskala ordinal.
-
Korelasi Kendall’s Tau (Kendall’s Tau Correlation)
Korelasi Kendall’s Tau adalah ukuran nonparametrik (uji statistik yang tidak memerlukan asumsi-asumsi mengenai persebaran data populasi), dari kuatnya dan arah hubungan yang ada antara dua variabel. Ukuran itu setidaknya pada skala ordinal.
Sifat-Sifat Koefisien Korelasi
Hasil dari analisis korelasi berupa indeks atau bilangan yang disebut dengan koefisien korelasi (r). Koefisien korelasi ini menunjukkan keeratan hubungan antar variabel. Hubungan yang terbentuk antar variabel dapat berupa hubungan positif, hubungan negatif, atau tidak memiliki hubungan. Arah korelasi ini dapat dilihat melalui nilai koefisien korelasi.
Nilai r sifatnya terbatas. Oleh karena itu, dikatakan bahwa koefisien korelasi merupakan sebuah norma yang batasnya adalah –1 ≤ r ≤ +1.
- r = +1
Menyatakan hubungan positif sempurna, dalam arti jika makin besar nilai x, semakin besar harga y, dan sebaliknya. Semua variasi yang terjadi pada y seratus persen bisa dijelaskan oleh variabel x.
- r = –1
Menyatakan hubungan negatif sempurna, dalam arti jika makin besar nilai variabel x, semakin kecil nilai variabel y, dan sebaliknya. Perubahan-perubahan pada variabel y seratus persen bisa diterangkan oleh perubahan-perubahan pada variabel x.
- r = 0
Menyatakan tidak ada hubungan antara variabel x dan variabel y atau mungkin modelnya bukan merupakan korelasi linier.
Koefisien korelasi r merupakan bilangan murni (pure number), artinya secara matematis r tidak memiliki satuan. Koefisien korelasi r menyatakan linier antara dua variabel. Oleh karena itu, sangat disarankan sebelum menghitung r dari data, terlebih dahulu gambarkan diagram pencar (scatter diagram) yang menggambarkan pola hubungan antara variabel x dan variabel y. Pembuatan diagram pencar tersebut dilakukan jika pola hubungan tidak dapat dihitung.
Setelah melakukan uji hipotesis dan hasilnya signifikan (berarti), maka untuk menentukan keeratan hubungan antara variabel x dan variabel y berdasarkan nilai r bisa digunakan Guilford’s Rule. Batas-batas nilai r sebagai berikut:
0,00 – 0,20 → korelasi yang sangat kecil dan bisa diabaikan
0,20 – 0,40 → korelasi yang sangat kecil dan tidak erat
0,40 – 0,70 → korelasi yang erat
0,70 – 1,00 → korelasi yang sangat erat
Macam-Macam Korelasi
- Korelasi Positif
Nilai koefisien korelasi positif menunjukkan titik-titik dalam diagram pencar berada di sekitar garis lurus regresi (garis linier) yang arahnya positif. Titik-titik tersebut makin dekat dengan garis lurus regresi makin mendekati nilai +1 berada pada garis lurus regresi.
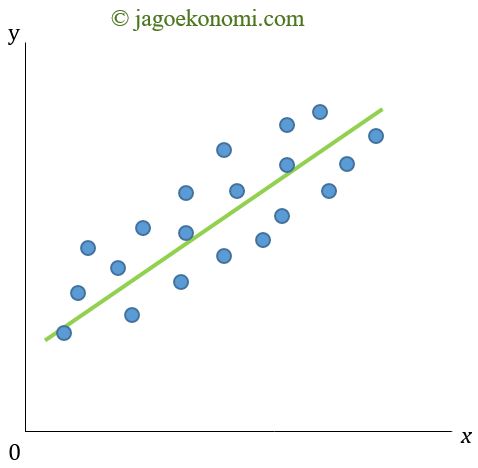
Perhatikan Gambar 1 di atas. Titik-titik yang membentuk garis lurus regresi positif atau titik-titik yang berada di sekitar garis lurus merupakan titik-titik yang menghubungkan nilai variabel x kecil dan nilai variabel y kecil pula, serta nilai variabel x besar dan nilai variabel y besar.
- Korelasi Negatif
Pada korelasi negatif, nilai variabel x yang besar berhubungan dengan nilai variabel y yang kecil, dan nilai variabel x yang kecil dengan nilai variabel y yang besar.
Pada Gambar 2 berikut, titik-titik akan berada pada sekitar garis lurus yang koefisien arahnya negatif. Jika titik-titik tersebut berada pada garis lurus yang arahnya negatif, nilai koefisien korelasinya adalah –1.
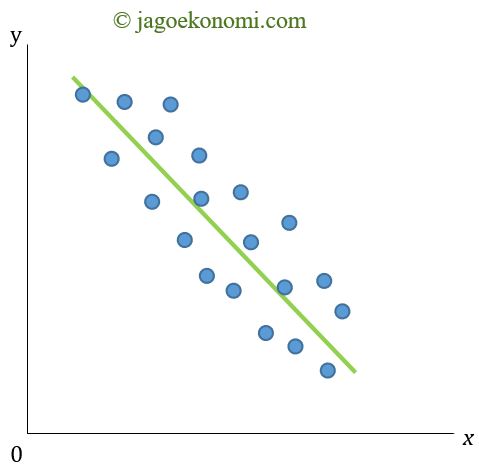
- Tidak Berkorelasi
Maksud tidak berkorelasinya antara variabel x dan variabel y adalah antara variabel x dan variabel y tidak terjadi/tidak ada hubungan. Artinya jika arah hubungan dua variabel tidak teratur, kadang-kadang searah, kadang-kadang berlawanan arah.
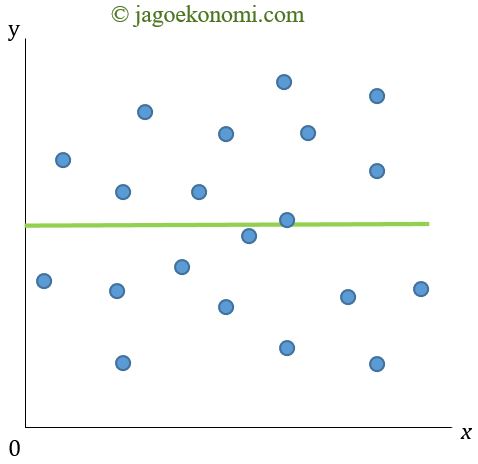
Gambar 3 di atas menunjukkan bahwa variabel x dan y tidak berkorelasi. Terlihat ketidakteraturan hubungan x dan y, dan tidak adanya pola hubungan antara variabel x dan variabel y.
Koefisien Determinasi
Nilai r yang mendekati +1 atau –1 menunjukkan hubungan yang semakin erat. Namun penafsiran keeratan hubungan berdasarkan besarnya nilai r kurang memberikan keterangan. Keterangan yang diperoleh akan lebih baik apabila penafsiran keeratan korelasi didasarkan pada koefisien determinasi dan didefinisikan sebagai r2.
Koefisien determinasi menunjukkan berapa besar perubahan pada variabel tak bebas (variabel y) yang bisa dijelaskan oleh variabel bebas (variabel x) melalui hubungan linier antara x dan y. Sebagai contoh, r = 0,90 ; r2 = 0,81. Artinya ialah bahwa 81% dari perubahan-perubahan yang terjadi pada variabel y bisa diterangkan oleh variabel x melalui hubungan linier tersebut. Sisanya diterangkan oleh variabel lainnya.
Dengan mengetahui hubungan antar dua variabel, dan seberapa erat hubungan tersebut, hal tersebut dapat menjadi bahan pertimbangan dalam mengambil keputusan atau menentukan kebijakan yang akan ditempuh.