Uji Asumsi Klasik Dalam Analisis Regresi

Analisis regresi merupakan salah satu alat yang sering digunakan untuk menganalisis banyak variabel secara bersamaan untuk menjawab pertanyaan penelitian yang kompleks. Analisis ini secara konseptual sebenarnya merupakan metode sederhana untuk memeriksa hubungan antar variabel. Hubungan antar variabel yang dimaksud tersebut digambarkan dalam bentuk persamaan atau model yang menghubungkan antara variabel dependen (Y) dan satu atau lebih variabel independen (X).

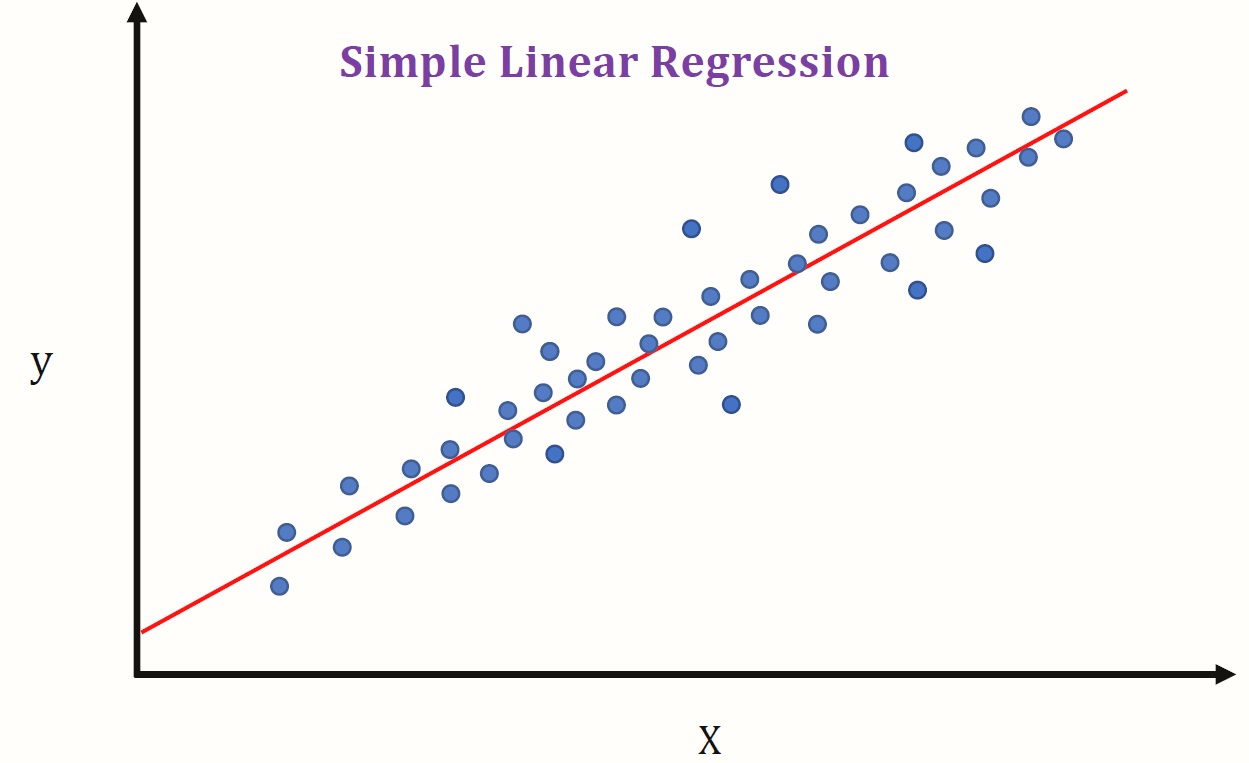
Model regresi linear yang terdiri dari satu variabel dependen dan satu variabel independen disebut dengan regresi linear sederhana (simple regression analysis). Sementara model regresi linear yang terdiri dari beberapa variabel independen dan satu variabel dependen disebut dengan regresi linear berganda (multiple regression analysis). 

Model regresi yang handal dan terpercaya ialah yang memenuhi kriteria BLUE (Best Linear Unbiased Estimator), yaitu model regresi yang bisa menghasilkan estimator yang tidak bias, konsisten, berdistribusi normal, dan juga efisien. Dan untuk mengetahui apakah model regresi yang digunakan telah memenuhi kriteria BLUE, maka perlu dilakukan serangkaian pengujian, yang kita kenal dengan Uji Asumsi Klasik.

Apa yang Dimaksud dengan Uji Asumsi Klasik?

Uji asumsi klasik adalah pengujian yang digunakan untuk menilai apakah di dalam sebuah model regresi linear yang berbasis ordinary least square (OLS) atau metode kuadrat terkecil, terdapat masalah-masalah asumsi klasik. Jadi regresi OLS ini mengasumsikan terdapatnya hubungan linear antara kedua variabel. Jika hubungannya tidak linear, regresi OLS bukan merupakan alat peramal yang valid untuk analisis penelitian, dan ini diperlukan suatu modifikasi pada variabel atau analisis tersebut.

Uji asumsi klasik ini merupakan uji prasyarat yang dilakukan sebelum melakukan analisis lebih lanjut terhadap data yang telah dikumpulkan. Dengan melakukan uji asumsi klasik, akan diketahui apakah model regresi itu baik atau tidak. Tujuan pengujian asumsi klasik adalah untuk memberikan kepastian bahwa persamaan regresi yang diperoleh memiliki ketepatan dalam estimasi, tidak bias, dan konsisten. Asumsi-asumsi yang harus dipenuhi dalam analisis regresi antara lain uji normalitas, linearitas, multikolinearitas, heteroskedastisitas, dan autokorelasi.

Uji Normalitas

Menurut Ghozali (2016), uji normalitas dilakukan untuk menguji apakah pada suatu model regresi, suatu variabel independen dan variabel dependen ataupun keduanya mempunyai distribusi normal atau tidak normal. Apabila suatu variabel tidak berdistribusi secara normal, maka hasil uji statistik akan mengalami penurunan.

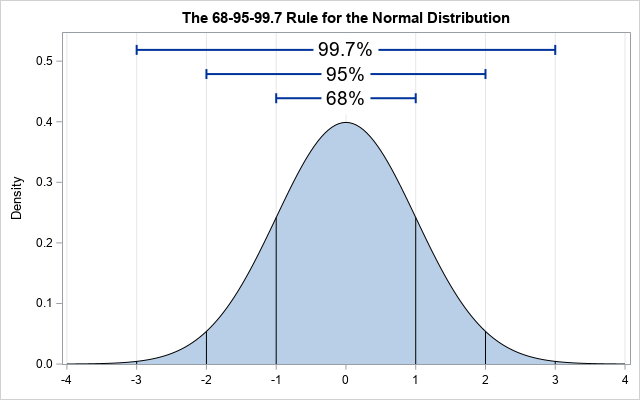
Uji normalitas dapat dilakukan dengan uji histogram, uji normal P-P Plot, Skewness dan Kurtosis, uji Jarque Berra, uji Shapiro-Wilk, dan uji One Sample Kolmogorov-Smirnov. Sebagai contoh, uji normalitas dengan normal probability-probability plot dilakukan dengan melihat penyebaran data (titik) pada sumbu diagonal grafik. Jika data menyebar di sekitar garis diagonal dan mengikuti arah garis diagonal atau grafik histogramnya menunjukkan pola distribusi normal, maka model regresi memenuhi asumsi normalitas.

Cara lain untuk menguji asumsi kenormalan ialah dengan melakukan uji Kolmogorov-Smirnov. Pada pengujian ini, kita dapat mengetahui apakah data penelitian memiliki distribusi yang normal atau tidak berdasarkan asumsi berikut:

• Data dikatakan berdistribusi normal apabila hasil uji Kolmogorov-Smirnov terhadap nilai residual dari analisis regresi linear, dihasilkan nilai signifikansi yang besarnya >0,05.

• Data dikatakan tidak berdistribusi normal apabila pada hasil uji Kolmogorov-Smirnov terhadap nilai residual dari analisis regresi linear, dihasilkan nilai signifikansi yang besarnya <0,05.

Uji Linearitas

Linearitas merupakan sifat hubungan yang linear antar variabel, yang berarti setiap perubahan yang terjadi pada satu variabel akan diikuti perubahan dengan besaran yang sejajar pada variabel lainnya. Uji linearitas dipergunakan untuk melihat apakah model yang dibangun mempunyai hubungan linear atau tidak. Pengujian ini melihat bagaimana variabel dependen mempengaruhi variabel independen, baik itu pengaruh berbanding lurus maupun berbanding terbalik.

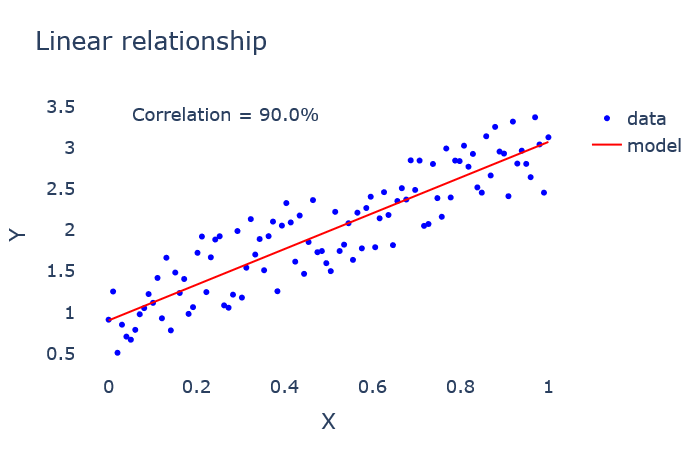
Seringkali uji linearitas tidak digunakan dalam beberapa studi, karena model-model yang dibentuk biasanya dibangun atas dasar studi teoritis bahwa hubungan antara variabel independen dan variabel dependen adalah linear. Hubungan antar variabel yang secara teoritis tidak menunjukkan hubungan linear, tidak dapat dianalisis dengan regresi linear. 

Jika ada hubungan antara dua variabel yang belum diketahui apakah linear atau tidak, uji linearitas tidak dapat digunakan untuk memberikan pernyataan bahwa hubungan tersebut bersifat linear atau tidak. Ia hanya digunakan untuk mengkonfirmasi apakah sifat linear antara dua variabel yang diidentifikasi dalam teori sesuai dengan hasil pengamatan. 

Secara umum, uji linearitas terbagi menjadi dua cara, yaitu analisis melalui grafik dan melalui uji statistik. Uji linearitas dapat dilakukan dengan menggunakan uji Durbin-Watson dan Ramsey Test.

Uji Durbin-Watson memang lebih dikenal untuk menguji autokorelasi, meskipun sebenarnya bisa juga digunakan untuk uji linearitas. Pengujian Durbin-Watson dilihat dengan membandingkan nilai Durbin Watson (DW) dan dL dalam tabel Durbin Watson dengan taraf signifikansi 5%. Kriteria keputusannya: apabila DW > dL, maka data berbentuk linear, dan apabila DW < dL maka data tidak berbentuk linear.   

Uji Multikolinearitas

Uji multikolinearitas digunakan untuk analisis regresi berganda, di mana terdapat lebih dari satu variabel independen. Model regresi yang baik tentunya tidak mengandung multikolinearitas. Kolinearitas terjadi ketika terdapat korelasi yang cukup tinggi di antara variabel independen. Uji multikolinearitas dirancang untuk menentukan apakah ada korelasi yang tinggi antara variabel independen dalam model regresi linear berganda.

Sebagai ilustrasi, misalnya kita akan meneliti bagaimana pengaruh besarnya pendapatan dan kekayaan terhadap tingkat konsumsi seseorang. Dalam hal ini pendapatan dan kekayaan ialah variabel independen, sedangkan tingkat konsumsi adalah variabel dependen. Seringkali antara pendapatan dan kekayaan memiliki korelasi yang cukup tinggi, sehingga menimbulkan multikolinearitas. Dampaknya terhadap model yaitu koefisien parsial regresi menjadi tidak terukur secara presisi. Oleh karena itu nilai standar eror menjadi besar.

   

 

Bila variabel-variabel bebas berkorelasi secara sempurna, maka metode kuadrat terkecil tidak bisa digunakan. Namun, apabila keterkaitan linear ini kurang sempurna, estimasi koefisien model regresi melalui kuadrat terkecil masih dapat diperoleh. Akan tetapi, estimasi ini cenderung tidak stabil; nilai-nilai ini dapat berubah dramatis dengan perubahan kecil pada data, dan lonjakan nilainya lebih besar dari yang diperkirakan.

Adanya multikolinearitas menyebabkan koefisien-koefisien individu mungkin memberikan tanda yang salah. Statistik t dalam penentuan signifikan masing-masing koefisien, kesemuanya mungkin tidak signifikan, tetapi uji F akan menunjukkan bahwa regresinya signifikan. Terakhir, penghitungan estimasi kuadrat terkecil sangat sensitif terhadap pembulatan galat.

Alat statistik yang biasanya digunakan untuk menguji adanya multikolinearitas adalah Variance Inflation Factor (VIF) dan nilai Tolerance. Nilai Tolerance mengukur variabilitas dari variabel bebas yang terpilih yang tidak dapat dijelaskan oleh variabel bebas lainnya. Nilai Tolerance memiliki hubungan erat dengan VIF, di mana VIF = 1/Tolerance. Ketika nilai Tolerance rendah maka nilai VIF akan tinggi. Hal ini menunjukkan adanya kolinearitas yang tinggi. Jadi, jika nilai Tolerance > 0,10 atau nilai VIF < 10, maka tidak terjadi multikolinearitas.

Uji Heteroskedastisitas

Uji heteroskedastisitas dilakukan untuk dapat menguji apakah model regresi memiliki keragaman eror yang sama atau tidak. Asumsi keragaman eror yang sama ini disebut dengan homoskedastisitas, sedangkan heteroskedastisitas yaitu terjadi jika keragaman nilai erornya tidak konstan atau berbeda. Hendaknya untuk dapat memenuhi kriteria BLUE, nilai eror pada setiap pengamatan nilainya konstan.  

Beberapa akibat yang ditimbulkan akibat adanya heteroskedastisitas antara lain:

1. Penaksir-penaksir OLS tidak akan bias (unbiased). 

2. Varian dari koefisien-koefisien OLS salah.

3. Penaksir-penaksir OLS akan menjadi tidak efisien.

Deteksi heteroskedastisitas dapat dilakukan dengan metode scatter plot dengan memplotkan nilai ZPRED (nilai prediksi) dengan SRESID (nilai residualnya). Model yang baik didapatkan jika tidak terdapat pola tertentu pada grafik, seperti mengumpul di tengah, menyempit kemudian melebar, atau sebaliknya melebar kemudian menyempit. Sementara itu metode statistik yang digunakan untuk mendeteksi heteroskedastisitas antara lain uji korelasi Rank-Spearman, Uji Goldfeld-Quandt, Uji Park, Uji Glejser, dan White General Heteroscedasticity Test.

Uji Autokorelasi

Autokorelasi adalah korelasi yang terjadi di antara anggota-anggota dari serangkaian pengamatan yang tersusun dalam rangkaian waktu (seperti pada data runtun waktu atau time series). Asumsi ini mengandung arti nilai-nilai faktor gangguan U yang berurutan tidak tergantung secara temporer, yaitu gangguan yang terjadi pada satu titik pengamatan-pengamatan yang dilakukan sepanjang waktu, pengaruh faktor gangguan yang terjadi dalam satu periode tidak terbawa ke periode berikutnya. 

Autokorelasi dalam sampel runtun waktu (time series sample) menunjukkan kecenderungan sekuler atau perubahan jangka panjang sepanjang waktu. Fluktuasi siklus juga memperlihatkan keteraturan pengamatan variabel yang berurutan sepanjang waktu, dan menjadi penyebab autokorelasi.  

Autokorelasi juga bisa diakibatkan oleh adanya bias spesifikasi, misalnya karena tidak dimasukkannya variabel-variabel benar dari persamaan regresi atau karena asumsi yang salah mengenai bentuk fungsional model regresi. Di samping itu, timbulnya masalah autokorelasi kadang-kadang karena salah satu variabel bebas dalam model regresi merupakan nilai lag (lagged value) dari variabel berikut. 

Akibat-akibat yang terjadi pada penaksir-penaksir apabila metode OLS diterapkan pada data yang mengandung autokorelasi:

1. Taksiran OLS tidak bias (unbiased).

2.  Varian dari taksiran OLS akan “underestimate”.

3. Peramalan akan tidak efisien (inefficient).

Pendeteksian autokorelasi secara grafis yaitu dengan melihat pola tebaran sisaan terhadap urutan waktu tidak membentuk suatu pola tertentu atau bersifat acak, maka dapat disimpulkan tidak ada autokorelasi antar sisaan. 

Menurut Gujarati, pengujian secara empiris dapat juga dilakukan dengan menggunakan statistik d Durbin-Watson yang dihitung berdasarkan jumlah selisih kuadrat nilai-nilai taksiran faktor-faktor gangguan yang berurutan. Nilai d dari Durbin-Watson diperoleh melalui rumus: 

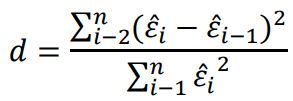
Kriteria keputusan dalam uji Durbin-Watson:

1. Jika d < d_L atau d > 4 – d_L, maka Ho ditolak, artinya terjadi autokorelasi.

2. Jika d_U < d < 4 – d_U, maka Ho diterima, artinya tidak terjadi autokorelasi.

3. Jika d_L ≤ d ≤ d_U  atau 4 – d_U ≤ d ≤ 4 – d_L, maka tidak dapat diputuskan apakah Ho diterima atau ditolak, sehingga tidak dapat disimpulkan ada tidaknya autokorelasi.